Keyword [Transformation] [Thin-Plate Spline (TPS)]
仿射变换与投影变换
数值方法——薄板样条插值(Thin-Plate Spline)
薄板样条函数(Thin plate splines)的讨论与分析
关于Thin Plate Spline (薄板样条函数)
1. 仿射变换
- 6个参数


2. 投影变换
- 8个参数. 通常采用z=1时的平面。

3. 薄板样条函数
3.1. 插值
已知函数y=f(x)在N+1个点x1, x2, x3, …上的函数值y1, y2, …,但是未知函数f(x). 可通过插值函数p(x)来逼近f(x).

常用的插值函数有
- 多项式函数 对于N次p(x)有N+1个参数,由于N+1个参数满足N+1个约束条件,因此可求出p(x). 但N阶多项式必有N-1个极值点,得到的插值函数摆动较大,类似过拟合现象。
- 样条函数 即分段函数,表示在相邻点x_{k}和x_{k+1}之间用低阶多项式S_{k}(x)进行插值。分段线性插值和三次样条插值都属于样条插值。
3.2. TPS (Thin plate splines)
- 寻找一个通过所有控制点的弯曲最小的光滑曲面

- 弯曲最小由能量函数定义

对于插值问题:自变量x是2维空间中的点,函数值y也是2维空间中的点,给定N个自变量x和对应函数值y,求插值函数
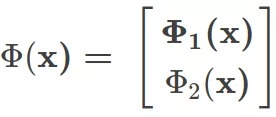
使得

- 即求两个插值函数φ。根据能量函数可得TPS插值函数形式

其中c是标量,向量a(2, 1),向量w(N, 1),函数向量

φ有N+3个参数,而目前只有N个约束(即y=φ(x),N对数据)。因此,添加三个约束

有

已知N对数据,即已知X和Y,也就是第1个矩阵和第3个矩阵,求第二个矩阵(薄板样条插值函数的参数)

令
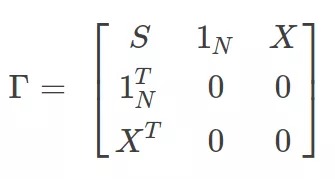
有

即可求得插值函数的参数。更进一步,可将x方向和y方向的插值函数φ通过一个矩阵运算计算

该逆矩阵称为弯曲能量矩阵
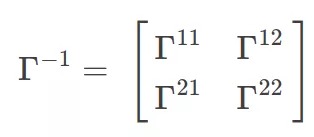
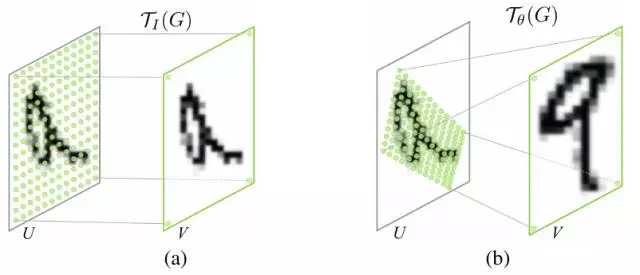
3.3. TPS应用在STN网络上

对于STN而言,已知
- 2维空间中的自变量x(第一个矩阵,根据尺寸超参数生成的标准网络中的点)
- 薄板样条(TPS)插值函数的参数(第二个矩阵,由Localization Network生成)
求
- 2维空间中的函数值y(第三个矩阵,标准网络经TPS变换后,得到的采样网格。即标准网格中的点映射到输入特征图或图像网格中的点)。