Keyword [Bilateral Filtering] [CRF] [Non-local Means]
如何轻松愉快地理解条件随机场(CRF)
非局部均值去噪(NL-means)
图像非局部均值滤波的原理
Bilateral Filtering(双边滤波) for SSAO
1. 条件随机场
- 对一系列连续时间段的照片分类时,为了提高分类器的性能,常常将相邻照片的标签信息考虑进来,而非单独考虑某张照片进行分类——条件随机场(CRF).
1.1. 词性标注中的特征函数
- 考虑对标注序列评分问题。定义CRF中的特征函数,如

- s 需要标注词性的句子
- i 句子s中第i个单词
- l_{i} 第i个单词标注的词性
- l_{i-1} 第i-1个单词标注的词性
- 特征函数输入0或1,0表示标注序列不符合特征函数的特征。该特征函数仅考虑当前单词i的标签与其前一个单词i-1的标签来进行判断,因此称为线性链CRF。
1.2. 特征函数到概率
- 定义好一组特征函数及其权重λ后,即可对标注序列进行评分。
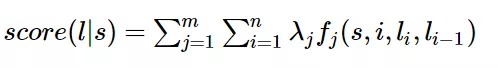
- 第一个Σ 所有特征函数对某个标注序列的评分求和
- 第二个Σ 某个特征函数对某个标注序列中每个单词的评分求和
- 进行指数化和标准化即可得到标注序列的概率值(属于某类的概率)

1.3. 特征函数例子
- l_{i-1}是介词,l_{i}是名词,则为1
- l_{i}为副词,且第i个单词以”ly”结尾,则为1
- 如果i=1,l_{i}为动词,且句子以”?”结尾,则为1
1.4. 与逻辑回归比较
CRF可看做逻辑回归的序列化版本。逻辑回归是用于分类的对数线性模型,CRF是用于序列化标注的对数线性模型。
与HMM比较
- HMM也能解决词性标注问题,其思路是生成方式。即已知标注序列的情况下,判断生成该标注序列的概率。

- p(l_{i} | l_{i-1}) 转移概率,如l_{i-1}=介词,l_{i}=名字,表示第i-1个词为介词,第i个词为名词的概率
- p(w_{i} | l_{i}) 发射概率,如l_{i}=名词,w_{i}=”ball”,表示第i个词为名字,则该词为”ball”的概率
- CRF比HMM强大,每个HMM模型都等价于某个CRF. 且CRF能解决许多HMM无法解决的问题。
- 对HMM取log

- 与CRF进行比较

- 如果把HMM中的概率看成CRF中的权重,可发现每个HMM转移概率能够定义成一个对应的CRF特征函数,并乘以权重(HMM的概率)。


- HMM中的发射概率同理。
- CRF优势
- CRF可定义大量不同的特征函数
- HMM具有局部性,只考虑当前单词i与其前一个单词i-1. CRF可定义具有全局性的特征函数
- HMM中的log概率值小于等于0,即转换成CRF后,其权重受到限制。而CRF中每个特征函数的权重可是任意值
2. 非局部均值去噪
- 基本思想:当前像素值的估计由图像中与其具有相似领域结构的像素加权平均得到。该算法能够在去噪的同时,最大程度保留图像细节特征。

2.1. 算法实现
- 理论上,该算法应搜索整个图像范围,但实际考虑到效率问题,会设定两个固定大小窗口。
- 搜索窗口(搜索范围)
- 邻域窗口(y为中心)
- 邻域窗口在搜索窗口中滑动,根据邻域间相似性确定各像素y的权值w(x,y)。

- 含噪声图像为v,去噪后的图像为u,其计算方式为
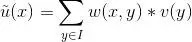
- 权值计算方式为

- V(y) 以y为中心的邻域.
- ||V(x) - V(y)||^2 两邻域间的距离
- Z(x) 归一化系数
- h 平滑参数,控制高斯函数的衰减成都,h越大,高斯函数变换越平缓,去噪水平越高,但图像越模糊。h取值应以图像中噪声水平作为依据
- 其中


3. Bilateral Filtering(双边滤波)
- 在滤波算法中,目标点的像素值通常由其周围邻域中的像素值所决定。
3.1. 2D高斯滤波
- 2D高斯滤波算法是对其一定范围的邻域内像素值赋以不同高斯权重值,进行加权平均。权重因子基于两像素点之间的空间距离得到,即离目标像素点距离越近,对最终结果贡献越大。


- ξ 邻域像素点坐标
- x 目标像素点坐标
- f 图像
- c(ξ, x) 基于两像素点空间距离的权重
- k_{d}(x) 单位化
- 但高斯滤波存在缺陷,只考虑了像素之间的空间位置关系,而没有考虑考虑像素值之间的相似程度,因此会导致边缘信息(图像中不同颜色的区域)丢失。
3.2. 基于像素值关系的权重
Bilateral中加入了另一部分权重


s(f(ξ), f(x)) 为基于两像素点的像素值相似关系的权重。
3.3. Bilateral滤波
- 综合考虑有


- 其中
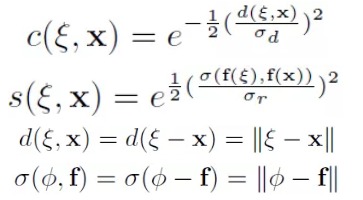
- 距离超过一定程度的像素点对目标像素点影响很小,可忽略。限定局部子区域后的离散化公式为
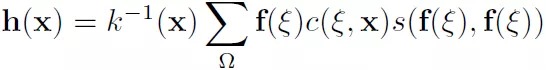
3.4. 可视化
- 对于带有噪声的图片

- 蓝框中心为目标像素所在位置,则其对应的高斯权重为

- 双边权重为

- 可看出Bilateral加入的相似程度部分将图像左侧与目标像素点的像素值差值过大的点滤去,从而保持了边缘。
- 进一步可视化,双边滤波后的图像为

- 原图像为

- 高斯滤波后的图像为

- 可看出高斯滤波后的图像存在线性变化边缘,即边界的丢失。而双边滤波后的图像保持了边缘梯度。