Keyword [SPADE]
Jiang L, Zhou Z, Leung T, et al. MentorNet: Regularizing Very Deep Neural Networks on Corrupted Labels[J]. arXiv preprint arXiv:1712.05055, 2017.
1. Overview
1.1. Motivation
- DNN can remember entire data which are labeled randomly
- DNN has more parameters than the number of training example
- Poor performance when overfit noise
- Curriculum Learning. gradually learn samples in a meaningful sequence
In this paper, it proposed MentorNet and SPADE (SG-partial-D) algorithm
- first study to learn a curriculum (weighting schema) from data by neural network
- supervise the training of StudentNet, improve the generalization on corrupted training data

- learn time-varying weights for each example to train StudentNet, result in a curriculum that decide the timing and attention to learning each example

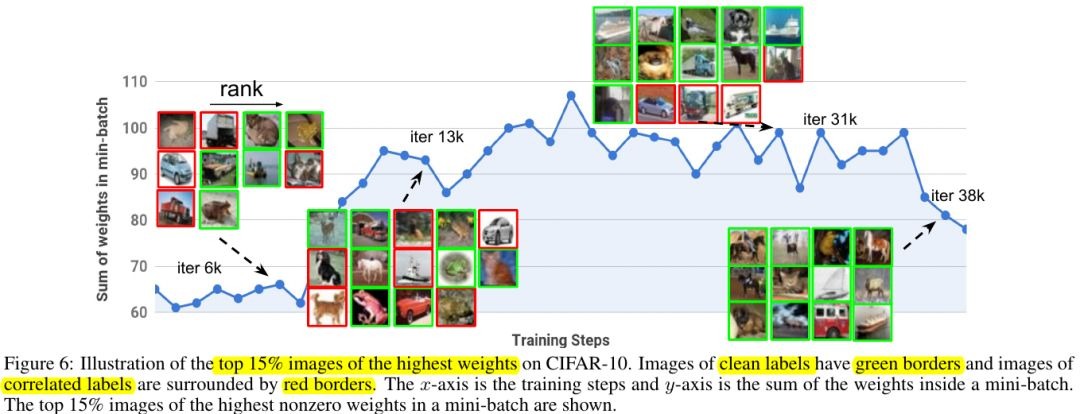
1.2. Step
- pretrain MentorNet to approximate predefined weighting specified in labeled data
- finetune MentorNet on the third clean label dataset
- train StudenNet using fixed MentorNet
- StudenNet make prediction without MentorNet
1.3. Related Work
1.3.1. Model Regularizer
- less effective on corrupted label.
- weight decay
- data augmentation
- dropout
1.3.2. Data Regularizer
tackle in the data dimension.
- MentorNet.
- foucs on weighting example in corrupted labels.
- can understand and further analyzed existing weighting schemes (self-paced weighting, hard negative mining, focal loss).
1.3.3. Weight Schemes
- Curriculum Learning
- Mine hard-negative example
- Training a network using clean data, coupled with a knowledge graph, to distill soft logits to the noisy data
1.4. Model
Goal
- overcome overfitting by introducing a regularizer to weight example
- alternately minimize w and v (fix one, update another)
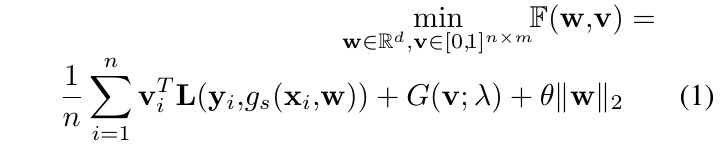
- Weighted Loss (WL)
- v (n samples x m classes). weight of examples
- L. loss
- g_{s}. StudentNet
- Explicit Data Regularizer (G). which contains two forms, both lead to same solution.
- explicit. analytic form of G(v)
- implicit. closed-form solution. v^{*} = argmin_{v} F(w, v) (F can be MentorNet)
- Weight Decay
1.5. Algorithm
- Problems
- fix v update w. wasteful when v is far away from optimal point
- fix w update v. matrix v is too large for memory
- SPADE
minimize w and v stochastically overmini-batches.

- (5) moving average on the p-th percentile
- (8) weight decay
- (9) SGD or other optim
2. MentorNet
2.1. Goal
- learn optimal Θ to compute the weight of example
- step. pretrain - finetune - fix and plug in Algorithm
2.2. Architecture
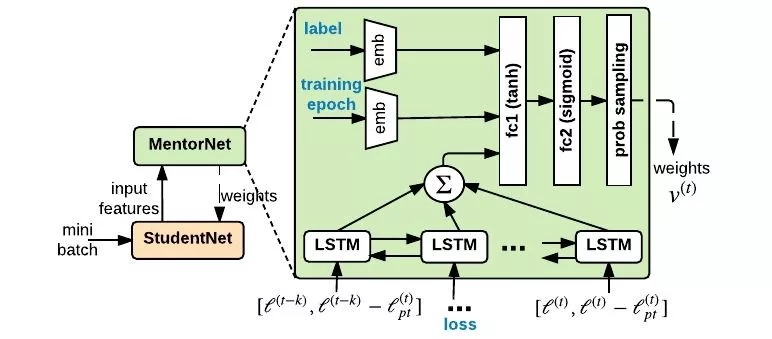

2.2.1. Input z
- label
- epoch
- absolute loss
- moving average
2.2.2. Sampling Layer
- sample the weights v, without replacement, according to the normalized weight distribution
- only perform on trained MentorNet
- sampling rate. hyperparameter
2.3. Pretraining
2.3.1. Dataset
- enumerate the input space of z, and annotate a weight for each data point
- weight can derived from any weight schemes
2.3.2. Objective Function
- (5). explicit
- (6). converge fast
- converge to the same solution

2.4. Finetuning
The weighting schemes may change along with the learning process of StudenNet.
- Dataset
- sample from dataset D
- binary label for whether learn this example
3. Experiments
3.1. Other network
- label weight according to different weighting schemes

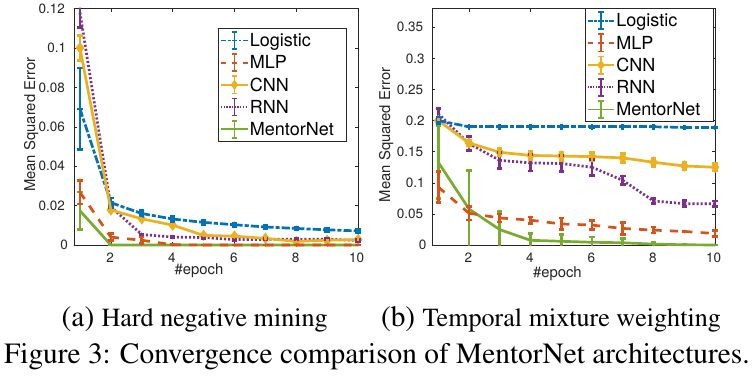
3.2. Other regularizer
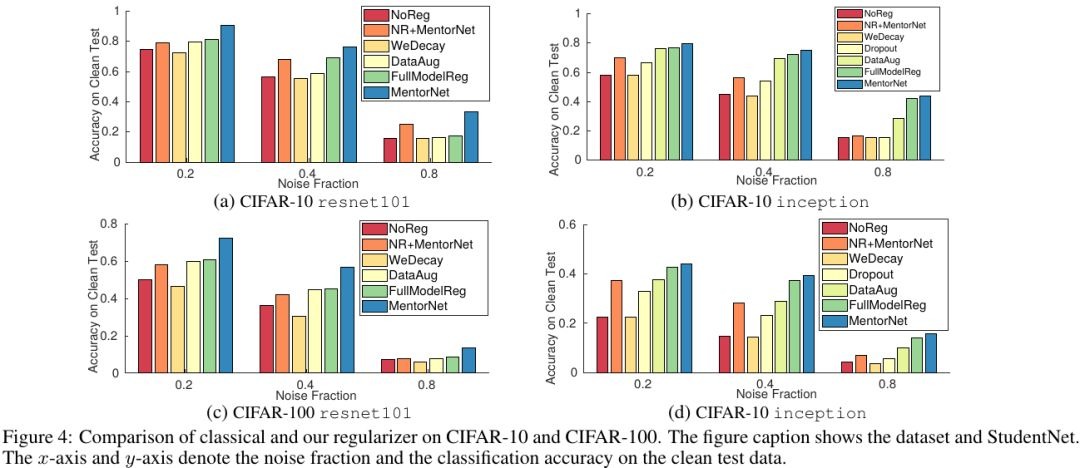

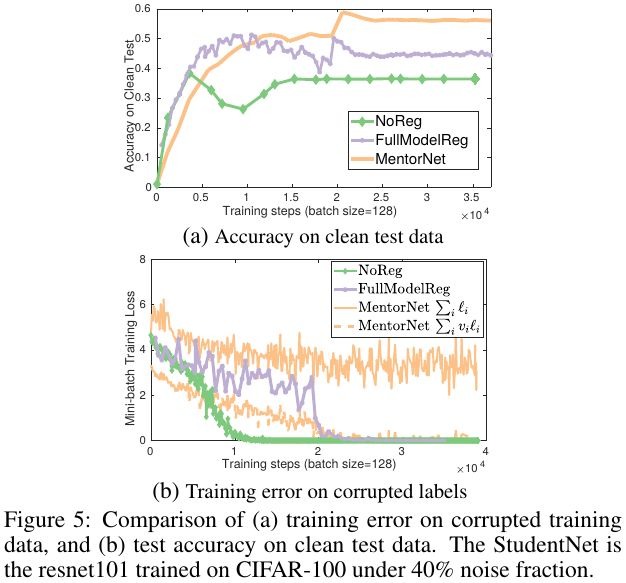
- (b). Weighted loss converge to zero
3.3. Representation of MentorNet
- similar images have less distance.
