Qi C R, Su H, Mo K, et al. Pointnet: Deep learning on point sets for 3d classification and segmentation[J]. Proc. Computer Vision and Pattern Recognition (CVPR), IEEE, 2017, 1(2): 4.
1. Overview
- Most method based on 3D voxel grids or collections of images, unnecessary and computation cost
- Point clounds are simple and unified structures, invariant to permutations.
In this paper, it proposed PointNet
- directly consumes unordered point clouds (xyz coordinate plus color etc)
- using symmetric function (maxpooling)
- using STN to aligned points
- learn critical points set (contribute to the results of maxpooling) and upper-bounded shapes (all point has nothing to do with maxpooling)

1.1. Contribution
- design PointNet for 3D point set
- exploit to classification, segmentation
- empirical and theoretical analysis on stability and efficiency
- illustrate 3D features computed by the selected neurons
1.2. Related Work
1.2.1. Point Cloud Feature
- handcrafted
1.2.2. Deep Learning on 3D Data
- Volumetric CNN
- FPNN
- Vote3D
- Multiview CNN
- Spectral CNN
- Feature-based DNN
1.2.3. DL on Unordered Set
1.3. Properties of Point Sets
- Unorderd. Invariant to permutation
- Interaction among points. neighbouring points form a meaningful subset
- Invariant under transformation. not modify the global point cloud category and segmentation of the points.
1.4. Network
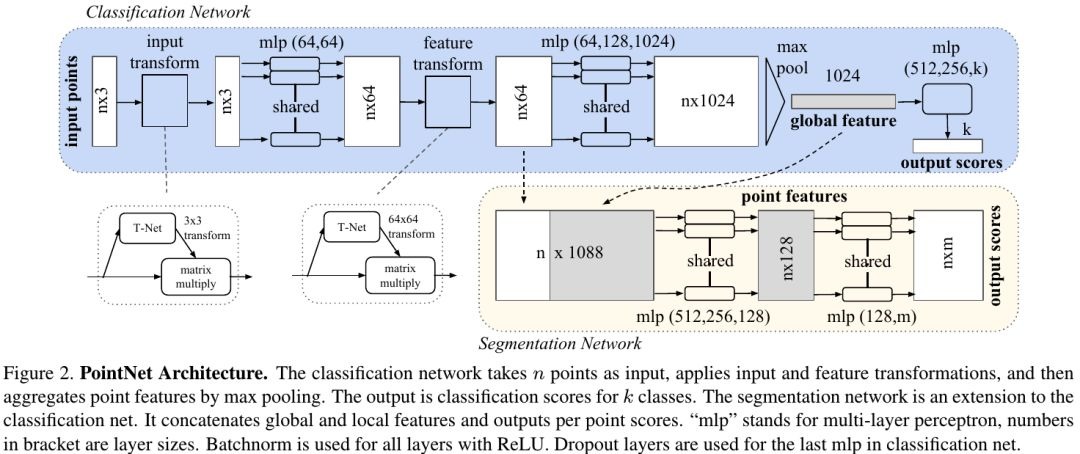
1.4.1. Three key modules
- maxpooling –> unordered
- a local and global information combination structure
Segmentation requires a combination of local and global knowledge. - two joint alignment networks
Transformation matrix in the feature space has much higher dimension (64*64) which greatly increase the difficulty of optimization. So constrain it to be close to orthogonal matrix
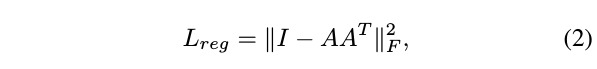
1.5. Formulation

- using g (maxpooling + single variable function) and h (MLP) to approximate f, so

- For two sets S and S’. the their distance is small, the mapping f of them is also similar
And f can be approximated by PointNet

If T (input corruption) contains the critical point set of S, it is unchanged. Based on this, if T contains some noise (not beyond upper-bounded shape), it is also unchanged
- critical point set only contains a bounded number of points (at most each K points contribute to one dimension of K dimensions global feature)
1.6. Dataset
- Classification. ModelNet40
- Part Segmentation. ShapeNet part dataset
- Semantic Segmentation. Stanford 3D semantic parsing dataset
2. Experiments
2.1. Classification
- uniformly sample 1024 points on mesh faces according to face area and normalize them into a unit sphere

2.2. Part Segmentation

2.3. Semantic Segmentation & Detection

- baseline. handcrafted point features
2.4. Order-Invariant Methods
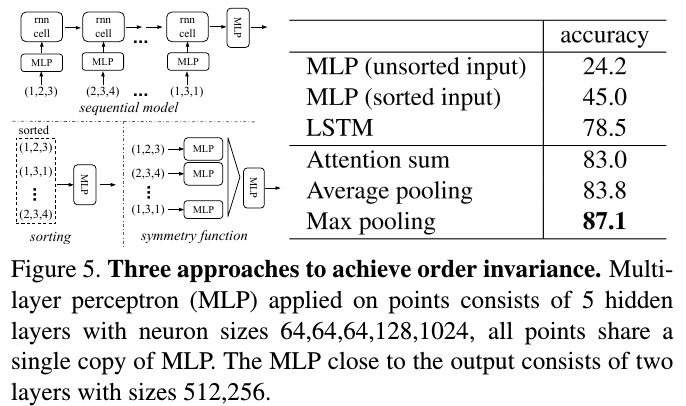
2.5. Alignment

2.6. Robust

2.7. Time and Space
