Keyword [Universal Adversarial Perturbations]
Khrulkov V, Oseledets I. Art of singular vectors and universal adversarial perturbations[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 8562-8570.
1. Overview
In this paper, it proposed a algorithm for constructing universal perturbation
- compute the (p,q)-singular vectors of the Jacobian matrices of hidden layers
- based on 64 images, the perturbation with more than 60% fooling rate on 50000 images dataset
- investigate a correlation between maximum singular value and fooling rate
1.1. (p-q)-singular gector

1.2. Jacobian
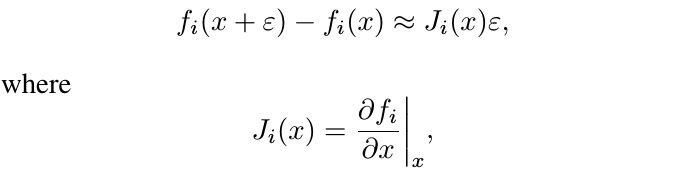
- f_i. the i-th hidden layer
- q-norm

- (p,q)-singular vector of J_i(x)
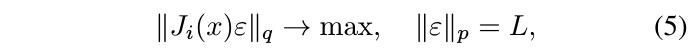
1.3. Iterative Methods
- Instead of evaluating and storing the full matrix A, we use only the macvec function of A (given an input vector v, computes an ordinary product Av without forming the full matrix A, O(n) complexity)
- Power Methods algorithm to compute (p,q)-singular vectors
1.4. Generalized Power Method


- x. ε
- A. Jacobian matrix
p,q. hyper-parameter
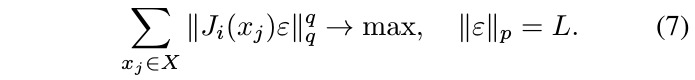
when stacking J vertically for each x_j

randomly choose a subset of images

1.5. Stochastic Power Methods
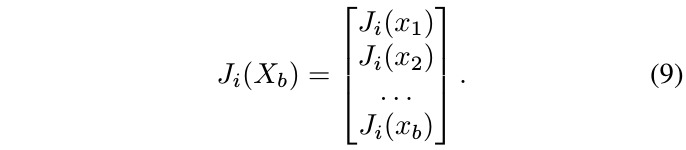

1.6. Efficient Implementation of the Matvec Function

1.7. Perturbation