Kohl S, Romera-Paredes B, Meyer C, et al. A probabilistic u-net for segmentation of ambiguous images[C]//Advances in Neural Information Processing Systems. 2018: 6965-6975.
1. Overview
1.1. Motivation
- many real-world vision problems suffer from inherent ambiguities which are common in medical imaging applications
- a group of graders typically produces a set of diverse but plausible segmentation
In this paper
- consider the task of learning a distribution over segmentations given an input
- propose generative segmentation modle (UNet+Conditional VAE) producing a unlimited number of plausible hypotheses
- experiments on LIDC-IDRI and Cityscape
1.2. Contribution
- the proposed framework provides consistent segmentation maps instead of pixel-wise probabilities
- induce arbitrarily complex output distributions including the occurrence of very rare modes
- sampling is computationally cheap
- allow quantitative performance evaluation
1.3. Dataset

1.3.1. LIDC-IDRI
- 4 annotation per input
- contain 1018 lung CT scans from 1010 lung patients with annotation from 4 experts (split to 772 patients train, 144 validation, 144 test)
- resample (0.5mm x 0.5mm) and cropped 2D images (180x180 pixels) centered at the lesion positions. get 8882 train, 1996 validation, 1992 test
1.3.2. Cityscapes
- total 19 different semantic classes
- create ambiguities by artifical random flips of five classes to newly introduced classes
- sidewalk to sidewalk2 with probability of 8/17
- person to person2 with 7/17
- car with 6/17
- vegetation with 5/17
- road with 4/17
- 500 test, split off 274 as validation from 2975 train
2. Methods

2.1. Prior Net & UNet
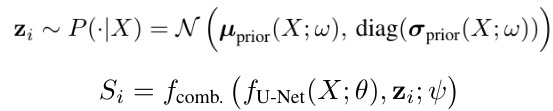
- w. parameters of prior net
- m. the number of segmentations to predict of an image X
- Θ. parameters of UNet
- f_comb. 1x1 Conv with parameters psi
- during m times, z and feature of UNet can be reused, only f_comb needs to be re-evaluated
2.2. Posterior Net
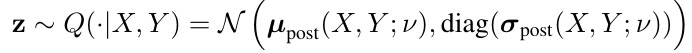
- v. parameters of posterior net, that learn to recognize a segmentation variant, given the raw image X and gt segmentation Y) and to map this to a position μ with some uncertainty sigma in the latent space
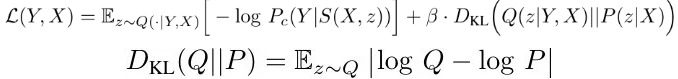
- S. prediction
2.3. Metric
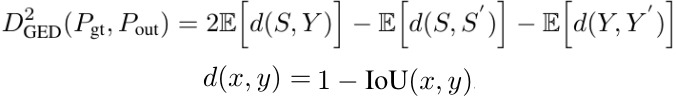
- Y, Y’. independent samples from gt distribution
- S, S’. independent samples from the predicted distribution
2.3.1. In LIDC
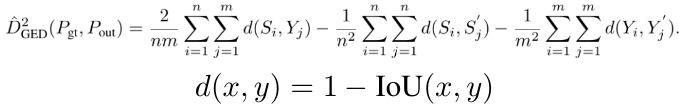
- m = 4. gt samples
- n samples from model
3. Experiments
3.1. Baseline

3.2. Comparison

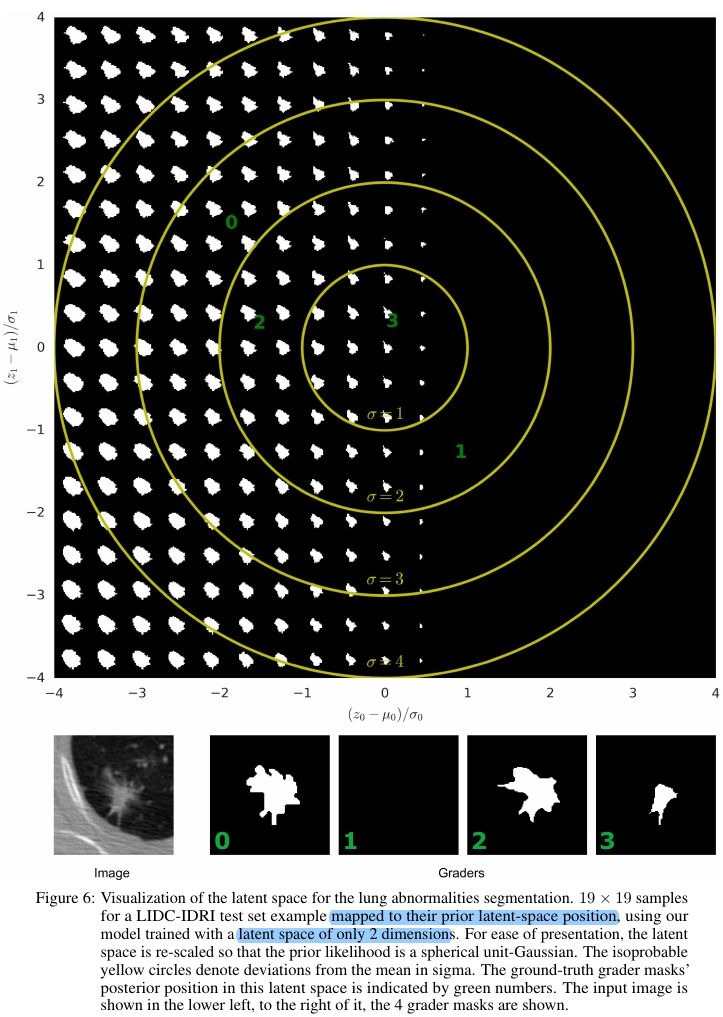
3.3. Visualization