Yang W, Li S, Ouyang W, et al. Learning feature pyramids for human pose estimation[C]//The IEEE International Conference on Computer Vision (ICCV). 2017, 2.
1. Overview
1.1. Motivation
- pyramid methods widely used at inference time
- learning feature in DCNN still not well explored
- existing weight initialization schemes (MSR, Xavier) are not proper for layers with branches

In this paper, it proposed Pyramid Residual Module (PRMs)
- subsample ratios in a multi-branch network
- weight initialization schemes
1.2. Contribution
- PRM
- weight initialization scheme
- observe that the problem of activation variance accumulation introduced by identity mapping may be harmful in some scenario
1.3. Related Work
1.3.1. Human Pose Estimation
- graph structures build on handcraft features. pictorial structure, loopy structure
- regression
- Gaussian peaks in score maps
- image pyramid. computation, memory
1.3.2. Multiple-layers of DCNN
- plain network. VGG, AlexNet
- multi-branch. inception, ResNet, ResNeXt
1.3.3. Weight Initialization
- layer-by-layer pretraining strategy
- Gaussian distribution. μ=0, σ=0.01
- Xavier. sound estimation of the variance of weight
- assume that weights are initialized close to zero, hence the nonlinear activation (sigmoid, Tanh) can be regarded as linear function
- initialization scheme for rectifier networks
- All above are derived for plain networks with only one branch.
1.4. Dataset
- MPII
- LSP
2. Framework
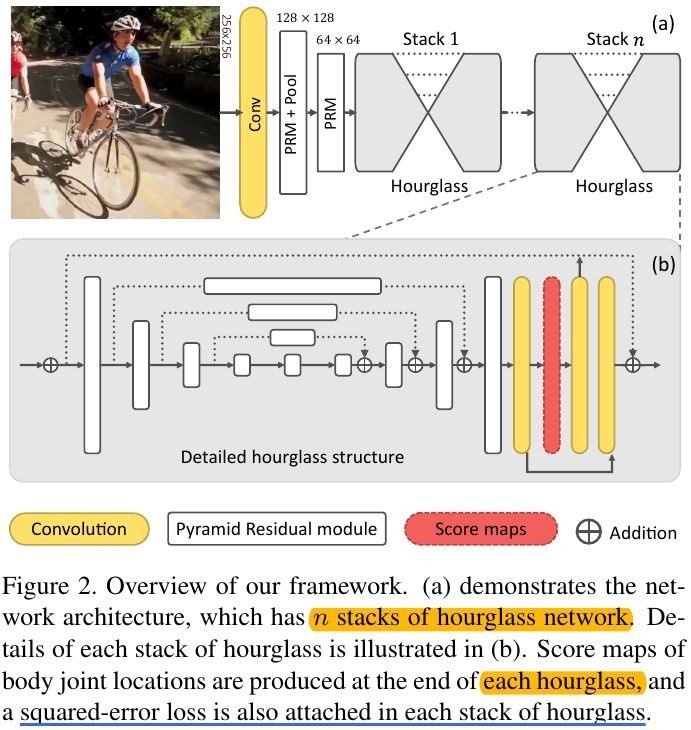
2.1. Pyramid Residual Modules

- PRM-B has comparable performance with others
- feature with smaller resolution contain relatively fewer information, we use fewer feature channels for branches with smaller scales

- C. the number of pyramid levels
- f_c. transformation for c-th pyramid level, design as bottleneck
2.2. Fractional Max-Pooling
- pooling reduces the resolution too fast
- fractional max-pooling to approximate the smoothing and subsampling process

- s_c. subsampling ratio ∈ [2^{-M}, 1]
- set M = 1, C = 4
3. Training and Inference
BN is less effective because of the small minibacth due to the large memory consumption of networks.
3.1. Loss Function

- for k-th body joint z_k=(x_k, y_k), ground-truth score map S_k is generated from a Gaussian with mean z_k and variance Σ
3.2. Forward Propagation
(Assumption μ=0)
To make the variances of the output y_l approximately the same for different layers, the condition must be satisfied

in initialization, a proper variance for W_l should be

α. depends on activation function, 0.5 for ReLU, 1 for Tanh and Sigmoid
- C_i. the number of input in l-th layers
- n_i. the number of elements in x_c, c=1,…, C_i
3.3. Backward Propagation

- C_o. the number of output
Special Case. C_o=C_i = 1 for plain network.
3.4. Output Accumulation
Drawbacks. identity mapping keeps increasing the variances of responses when the network goes deeper, which increase the difficulty of optimization.

- the identity mapping will be replaced by Conv to reduce or increase the channels, which can reset the variance to small value

- 1x1 Conv-BN-ReLU to replace identity mapping, which can stops the variance explosion
- find that breaking the variance explosion can provide a better performance


4. Experiments
4.1. Details
- 256x256 cropped
- scaling, rotation, flipping and adding color noise
- mini-batch 16
- test. six-scale pyramid with flipping
4.2. Comparison

4.3. Ablation Study
4.3.1. Variant

4.3.2. Scale of Pyramid and Weight initialization

4.3.3. Controlling Variance Explosion
- [w]88.5 vs [w/o]88.0 vs [baseline] 87.6