Keyword [ImageNet-C] [ImageNet-P] [Image Corruption]
Geirhos R, Rubisch P, Michaelis C, et al. ImageNet-trained CNNs are biased towards texture; increasing shape bias improves accuracy and robustness[C]. international conference on learning representations, 2019.
1. Overview
In this paper, it proposes two Benchmark Dataset
1) ImageNet-C (Different Corruption).
2) ImageNet-P (Perturbation Sequence).
3) Evaluation Metric.
4) Protocal: Allow train with other distortions (e.g., uniform noise), standard data augmentation (cropping, flipping)
2. Definition
1) Corruption Robustness ($E_{c \sim C}[P_{(x,y) \sim D} (f(c(x) = y))]$).
2) Perturbation Robustness ($E_{\mathcal{e} \sim \mathcal{E}}[ P_{(x,y) \sim D}(f(\epsilon (x)) = f(x)) ]$)
3. ImageNet-C

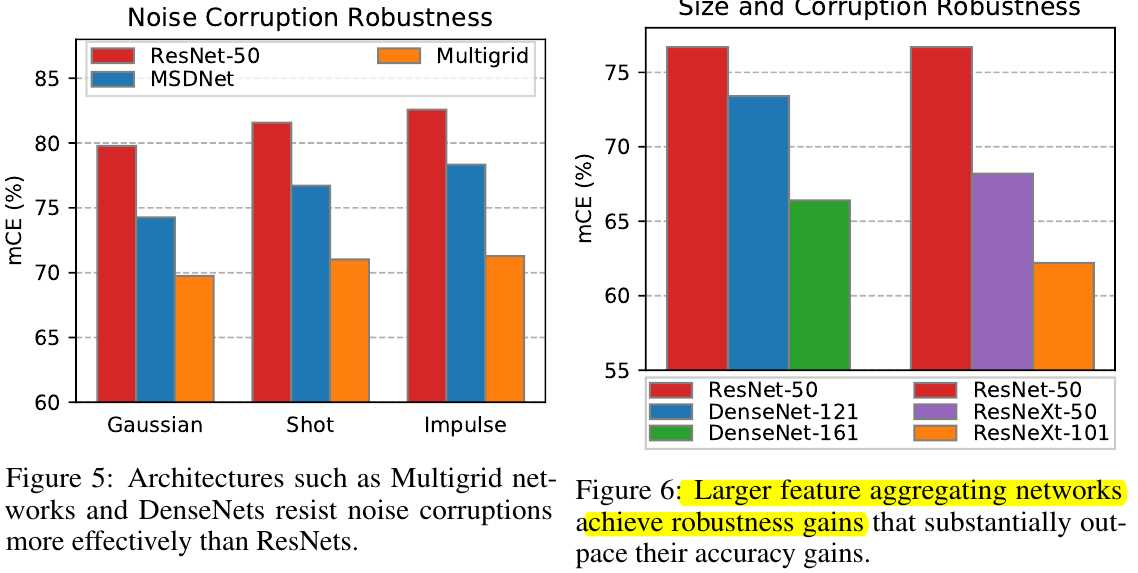
1) Four main categories Corruptions: Noise, Blur, Weather, Digital.
2) Each corruption type has five levels of severity. (Total 75 ($15 \times 5$) corruptions)

3.1. Common Corruption
1) Gaussian Noise. Appear in low-lighting conditions
2) Shot Noise (Poisson Noise). Electronic noise caused by discrete nature of light
3) Impulse Noise. Color analogue of salt-and-pepper noise caused by bit error.
4) Defocus Blur. Out of focus
5) Frosted Glass Blur. Appear with “frosted glass” windows or panels.
6) Motion Blur. Camera moves quickly
7) Zoom Blur. Camera moves toward an object rapidly
8) Snow.
9) Frost. lenses or windows are coated with ice crystals.
10) Fog.
11) Brightness.
12) Contrast.
13) Elastic.
14) Pixelation. upsample low-resolution images
15) JPEG.

3.2. Mean Corruption Error (mCE)
$CE_c^f = ( \Sigma_{s=1}^5 E_{s,c}^f - E_{clean}^f ) / ( \Sigma_{s=1}^5 E_{s,c}^{AlexNet} - E_{clean}^{AlexNet} )$
1) $c$. Corruption type
2) $s$. Level of severity
3) $f$. Network
4. ImageNet-P

1) Like ImageNet-C, consists of noise, blur, weather and digital distortions.
2) Departs from ImageNet-C, ImageNet-P having perturbation sequences (more than 30 frames).
3) Apart from Gaussian Noise, the remaining perturbation sequences have temporality. Each frame is a perturbation of the previous frame.
4) The perturbation sequences with temporality are created with motion blur, zoom blur, snow, brightness, translate, rotate, tilt and scale perturbations.
4.1. Mean Top-5 Distance (mT5D)
$S = {( x_1^{(i)}, x_2^{(i)}, …, x_n^{(i)}, )}_{i=1}^m$
4.1.1 Top-1
1) For other perturbation sequences:
$FP_p^f = \frac{1}{m(n-1)} \sum_{i=1}^m \sum_{j=2}^n \mathbf{1} (f(x_j^{(i)} \ne f(x_{j-1}^{(i)})) = \mathbf{P}_{x \sim S} (f(x_j) \ne f(x_{j-1})).$
2) For noise perturbation sequences:
$FP_p^f = \frac{1}{m(n-1)} \sum_{i=1}^m \sum_{j=2}^n \mathbf{1} (f(x_j^{(i)} \ne f(x_{1}^{(i)})) = \mathbf{P}_{x \sim S} (f(x_j) \ne f(x_{1}) | j \gt 1) .$
3) Flip Rate: $FR_p^f = FP_p^f / FP_p^{AlexNet}$.
4.1.2 Top-5
1) For other perturbation sequences:
$uT5D_p^f = \frac{1}{m(n-1)} \sum_{i=1}^m \sum_{j=2}^n d(\tau(x_j), \tau(x_{j-1})) = \mathbf{P}_{x \sim S} (d(\tau (x_j), \tau (x_{j-1})))$
(a) $\tau$. Permutation of prediction rank.
(b) $d$. L1 distance.
2) For noise perturbation sequences:
$uT5D_p^f = \mathbf{E}_{x \sim S} [d(\tau (x_j), \tau (x_1)) | j \gt 1 ]$.
3) $T5D_p^f = uT5D_p^f / uT5D_p^{AlexNet}$
5. Experiments