Keyword [Global Context Block]
Cao Y, Xu J, Lin S, et al. GCNet: Non-local Networks Meet Squeeze-Excitation Networks and Beyond[J]. arXiv preprint arXiv:1904.11492, 2019.
1. Overview
1.1 Motivation
Global contexts modeled by Non-local are almost the same for different query positions.

In this paper
1) Simplify NL block and propose Global Context Modeling Framework (3 steps).
2) Propose Global Context (GC) Block.
3) Experiments with stronger backbone (Deformable Conv).
2. Analysis on Non-local Networks
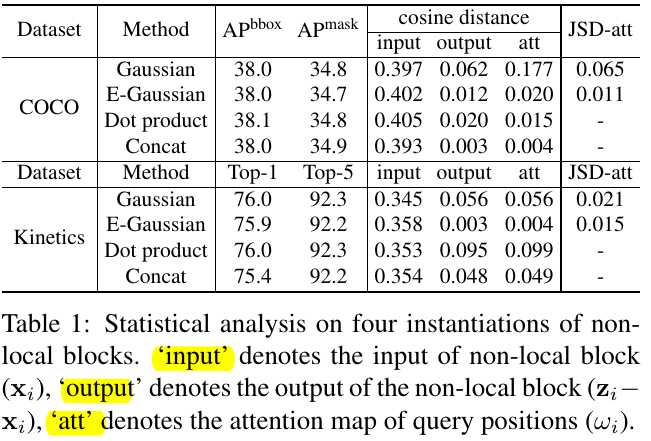
$AvgDist=\frac{1}{N_p^2}\Sigma_{i=1}^{N_p} \Sigma_{j=1}^{N_p} dist(v_i, v_j)$.
1) $v_i$. the feature vector for position $i$, total $N_p$ positions.
2) The distances of ouput and att are quite small, so the global context is actually independent of query position. There is no need to compute query-specific global context for query position.
3. Methods
3.1. Simplify Non-local

1) $z_i = x_i + \Sigma_{j=1}^{N_p} \frac{exp(W_kx_j)}{\Sigma_{m=1}^{N_p}exp(W_kx_m)}(W_v \cdot x_j)$
2) To further reduce computation. $z_i = x_i + W_v \Sigma_{j=1}^{N_p} \frac{exp(W_kx_j)}{\Sigma_{m=1}^{N_p}exp(W_kx_m)}x_j$
3.2. Global Context Modeling Framework

3 steps:
1) Context Modeling.
2) Transform.
3) Fusion.
3.3. Global Context Block
1) In Transform model, replace $1 \times 1 Conv$ ($C \cdot C$) with Bottleneck ($2 \cdot C \cdot C/r$).
2) Add LayerNorm in Transform.
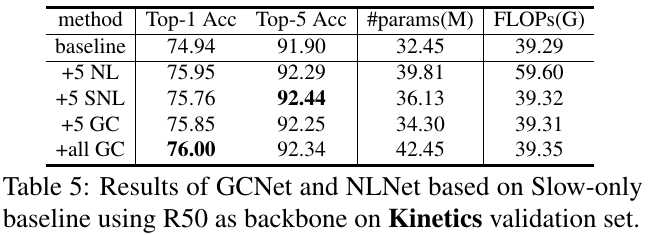
4. Experiments
Stronger backbone with Deformable Conv.
4.1. Ablation Study
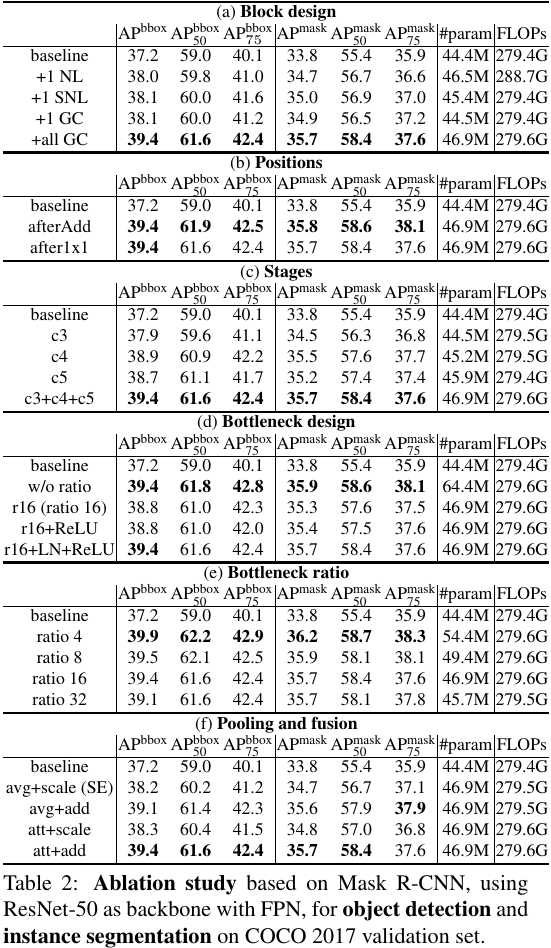

4.2. Experiments