Keyword [Facial Landmarks] [Makeup Transfer]
Jiang W, Liu S, Gao C, et al. PSGAN: Pose-Robust Spatial-Aware GAN for Customizable Makeup Transfer[J]. arXiv preprint arXiv:1909.06956, 2019.
1. Overview
1.1. Motivation
Existing GAN-based methods
1) Fail in cases with variant poses and expression.
2) Can not adjust the shade if makeup.
3) Can not specify the part of transfer.
In this paper, it proposes Pose-robust Spatial-aware GAN (PSGAN) for transferring makeup styles.
1) Makeup Distillation Network (MDN). Extract two makeup matrices $\gamma$ and $\beta$ from Reference the image $y$.
2) Attentive Makeup Morphing Module (AMM). Morph $\gamma’$ and $\beta’$.
3) De-makeup Re-makeup Network (DRN). Apply $\gamma’ and \beta’$ to Source image $x$.
4) Facial Mask (lip, eye, skin) combine with $\gamma’$ and $\beta’$ to implement part-by-part or interpolation.
5) 68 facial landmarks are exploited to improve performance.

1.2. Analysis
1) Pose-robust → AMM.
2) Part-by-Part → Facial Mask.
3) Controllable Shade → weight $[0,1]$ of $\gamma’$ and $\beta’$.
2. PSGAN
1) Source image domain $X = \lbrace x_n \rbrace_{n=1,…,N}, N=1115$.
2) Reference image domain $Y = \lbrace y_m \rbrace_{m=1,…,M}, M=2719$.
2.1. Framework

MDN disentangles makeup related features (lip gloss, eye shadows) for intrinsic facial features (facial shape, eye size).
1) MDN extracts makeup related features $\gamma$ and $\beta$ from $y_m$.
2) AMM morphs $\gamma$ and $\beta$ to $\gamma’$ and $\beta’$.
3) DRN de-makeups $x_n$ (same encoder as MDN, but not share) into $V_x$.
4) Apply $\gamma’$ and $\beta’$ to $V_x$, get $V_x’$.
5) DRN (re-makeups) decodes $V_x’$.
2.2. AMM
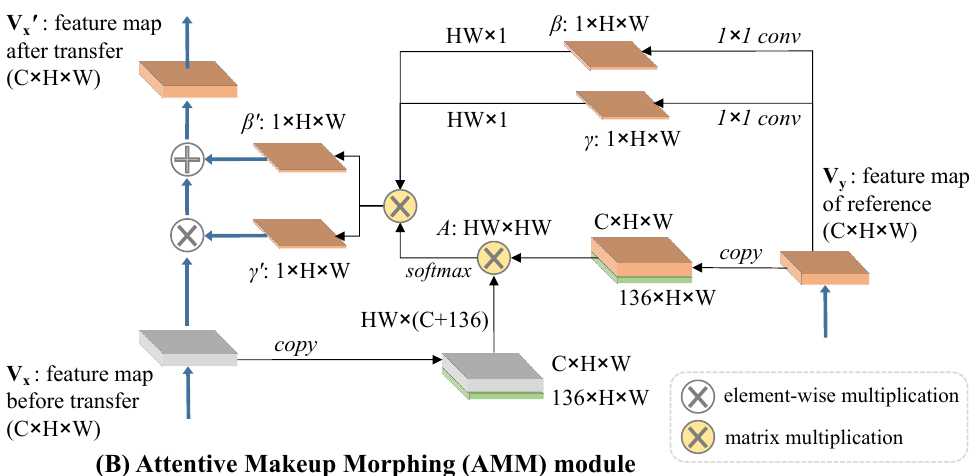
1) Concat visual features with relative position vectors (68 facial landmarks) $p \in R^{126}$.
$p_i = [f(x_i) - f(l_1), …, f(x_i) - f(l_{68}), g(x_i) - g(l_1), …, g(x_i) - g(l_{68})]$ ($f,g$ means $x,y$ axes)
2) To avoid unreasonable sampling pixels with similar relative positions but different semantics, also consider visual similarity.
$A_{i,j} = \frac{exp([v_i,p_i]^T[v_j,p_j]) I(m_x^i=m_y^j)}{\Sigma_i exp([v_i,p_i]^T[v_j,p_j]) I(m_x^i=m_y^j)}$
3) When calculate $A$, we only consider the pixels belonging to same facial region.
$m_x, m_y \in \lbrace 0, 1, …, N-1 \rbrace^{H \times W}, N=3$ (eye, lip, skin)
2.3. Loss Function
1) $L_D = \lambda_{adv} L_D^{adv}$.
2) $L_G = \lambda_{adv} L_G^{adv} + \lambda_{cyc}L_G^{cyc} + \lambda_{per}L_G^{per} + \lambda_{make}L_G^{make}$
a) Adversarial Loss
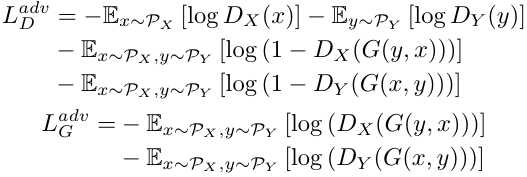
b) Cycle Consistency Loss
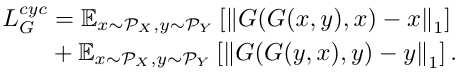
c) Perceptual Loss
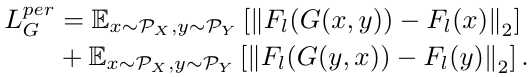
d) Makeup Loss
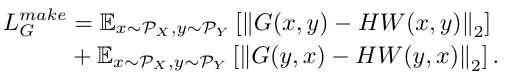
1) Histogram Match $HW(x,y)$ preserves identity of $x$ and shares a similar color distribution with $y$.
3. Experiments
3.1. Details
1) $lambda_{adv}=1, lambda_{cyc}=10, lambda_{per}=0.005, lambda_{make}=1$.
2) 50 epoches, batch size 1, Adam 0.0002.
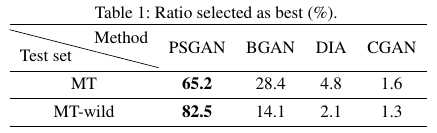
3) Human evaluation metric.
4) Makeup Transfer Dataset.
3.2. Ablation Study

3.3. Partial and Interpolated Makeup
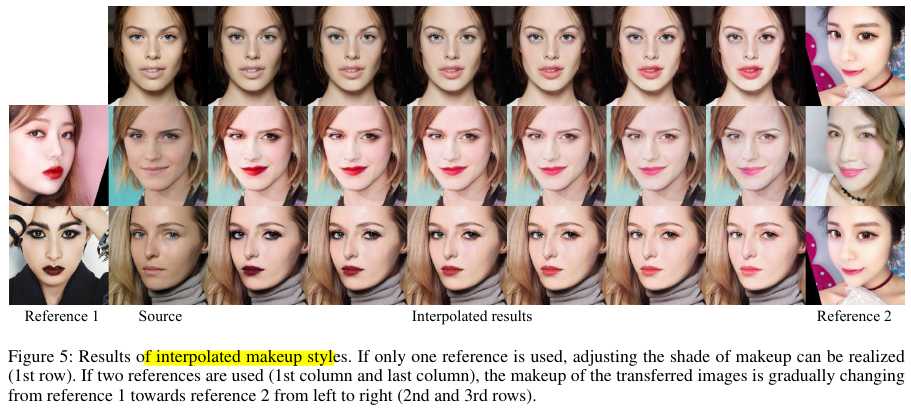
$V_x’ = ( (1-m_x)\Gamma_x’ + m_x \Gamma_y’)V_x + ( (1-m_x)B_x’ + m_xB_y’ )$
3.4. Mixed Makeup

$V_x’ = ( (1-\alpha)\Gamma_{y_1}’ + \alpha \Gamma_{y_2}’)V_x + ( (1-\alpha)B_{y_1}’ + \alpha B_{y_2}’ ), \alpha \in [0,1]$
3.5. Comparision