Huang X, Liu M Y, Belongie S, et al. Multimodal unsupervised image-to-image translation[C]//Proceedings of the European Conference on Computer Vision (ECCV). 2018: 172-189.
1. Overview
In this paper, it proposes a Multimodal Unsupervised Image-to-Image Translation (MUNIT)) framework.
1) Decompose image into a content code (shared space) and a style code (different space).
2) Recombine content and style to restore image or transer.

2. MUNIT
2.1. Procedure

1) Encoder $E_i$ and Decoder $G_i$ for each domain $X_i (i=1, 2)$.
2) $(c_i, s_i) = (E_i^c(x_i, ), E_i^s(x_i)) = E_i(x_i)$.
3) Translation $x_{1 \to 2} = G_2(c_1, s_2),$ $where$ $c_1 = E_1^c(x_1); q(s_2) \sim N(0, I)$
2.2. Loss Function
$min_{E_1, E_2, G_1, G_2} max_{D_1, D_2}$ $L(E_1, E_2, G_1, G_2, D_1, D_2) = L_{GAN}^{x_1} + L_{GAN}^{x_2} +$
$\lambda_x (L_{recon}^{x_1} + L_{recon}^{x_2}) + \lambda_c (L_{recon}^{c_1} + L_{recon}^{c_2}) + \lambda_s (L_{recon}^{s_1} + L_{recon}^{s_2})$.
1) Image Reconstruction Loss
$L_{recon}^{x_1} = E_{x_1 \sim p(x_1)}[\lVert G_1 (E_1^c(x_1),E_1^s(x_1)\rVert_1]$.
2) Latent Reconstruction Loss
$L_{recon}^{c_1} = E_{c_1 \sim p(c_1), s_2 \sim q(s_2)}[\lVert E_2^c (G_2(c_1, s_2)) - c_1 \rVert_1 ]$
$L_{recon}^{s_2} = E_{c_1 \sim p(c_1), s_2 \sim q(s_2)}[\lVert E_2^s (G_2(c_1, s_2)) - s_2 \rVert_1 ]$
3) Adversarial Loss
$L_{GAN}^{x_2} = E_{c_1 \sim p(c_1), s_2 \sim q(s_2)} [ log(1 - D_2(G_2(c_1, s_2))) ] + E_{x_2 \sim p(x_2)} [ log D_2(x_2) ]$
2.3. Details

1) Content Encoder. All Conv follow by0 IN.
2) Style Encoder. Do not use IN, since IN removes the original feature mean and variance that represent important style information.
3) Decoder. Equip ResBlock with AdaIN.
$AdaIN(z, \gamma, \beta) = \gamma (\frac{z - \mu(z)}{\sigma(z)}) + \beta$.
$\gamma, \beta$ are parameters generated by the NLP.
3. Experiments
3.1. Metric
1) Human Preference. AMT
2) LPIPS Distance.
3) (Conditional) Inception Score.
$CIS = E_{x_1 \sim p(x_1)} [ E_{x_{1 \to 2} \sim p(x_{2 \to 1} | x_1)} [ KL(p(y_2 | x_{1 \to 2}) \lVert p(y_2 | x_1)) ] ]$
$IS = E_{x_1 \sim p(x_1)} [ E_{x_{1 \to 2} \sim p(x_{2 \to 1} | x_1)} [ KL(p(y_2 | x_{1 \to 2}) \lVert p(y_2)) ] ]$
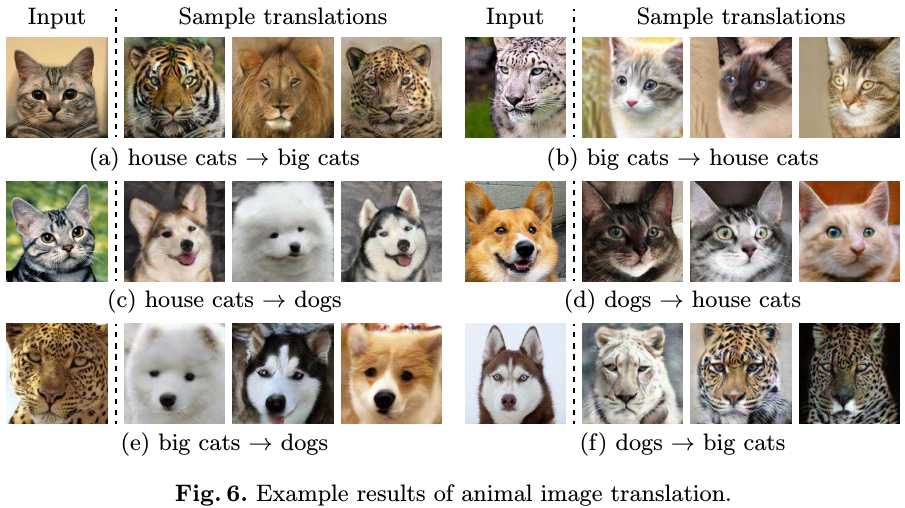
3.2. Visualization